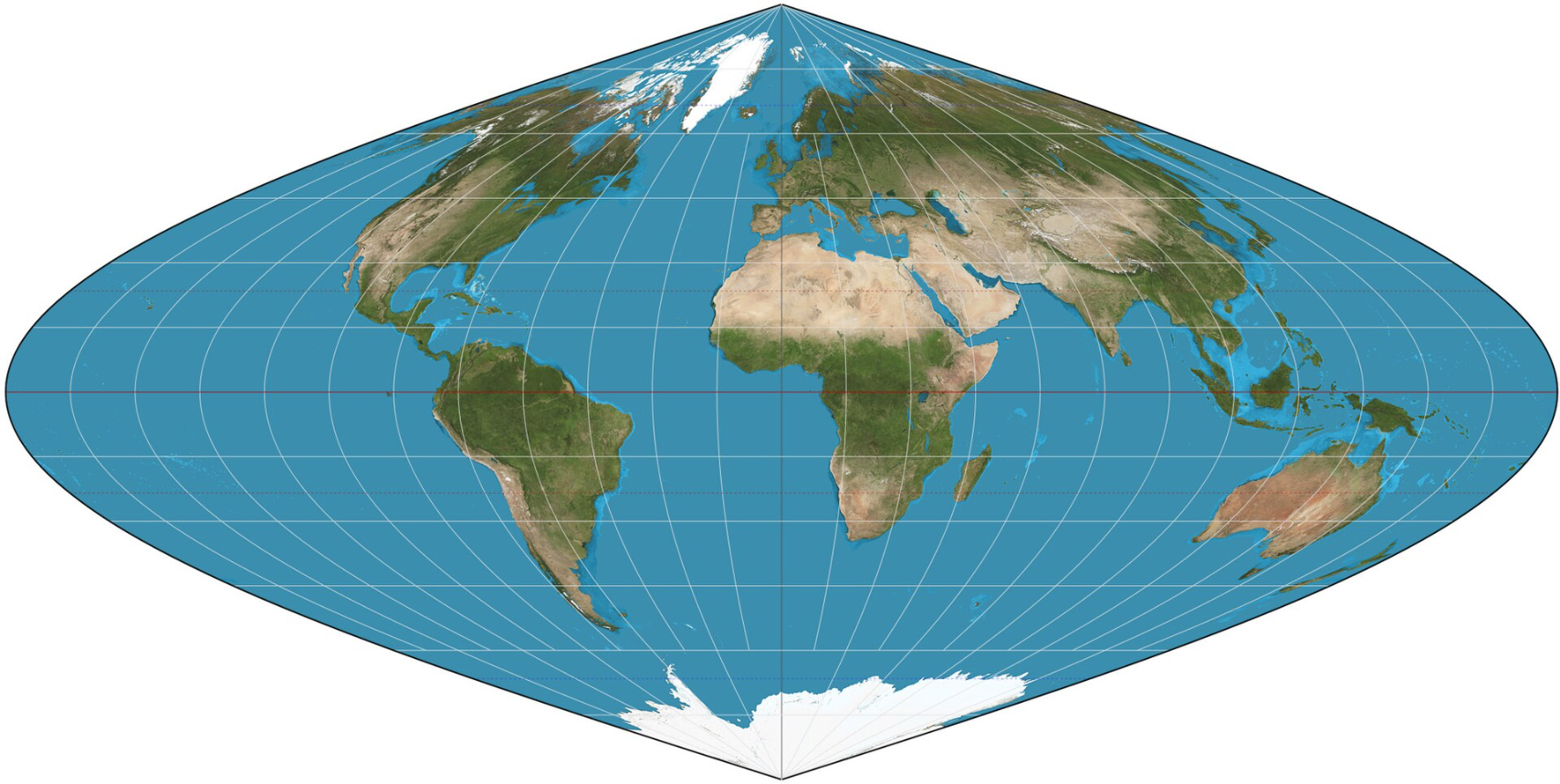
Gauss–Krüger Projection
Gauss–Krüger projection is a map projection based on the Transverse Mercator projection, developed by the German geographers Carl Friedrich Gauss and Johann Heinrich Krüger. It is widely used for large-scale topographic maps and precision surveying, and is adopted as part of the national coordinate system by many countries, notably Germany, Russia, and China.
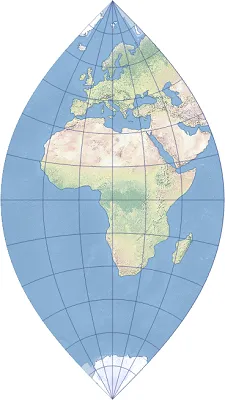
2025-09-16 14:47:00Lambert Azimuthal Equal-Area Projection
Lambert Azimuthal Equal-Area Projection is an equal-area azimuthal projection proposed by German mathematician Johann Heinrich Lambert in 1772. This projection maps points on the earth’s surface onto a plane through spherical projection, keeping the projection area unchanged, that is, the area ratio of the area before and after the projection is strictly equal. There is no deformation at the center of the projection, and as the distance from the center increases, the angle and shape deformation gradually increase, but the area deformation is always zero.
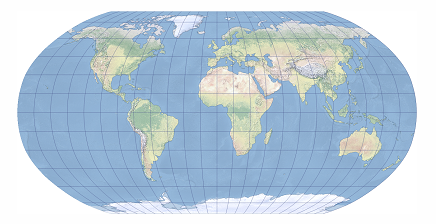
2025-09-16 14:47:00Robinson Projection
Robinson projection is a compromise projection designed by Arthur H. Robinson in 1963 at the request of the Rand McNally Company. It was developed using graphic design rather than mathematical equations to provide a balanced visual effect for world maps. The projection is a pseudo-cylindrical projection. The meridians are regularly distributed curves that imitate elliptical arcs. They are concave to both sides with the central meridian as the center and do not intersect the parallels perpendicularly. The parallels are unequally distributed straight lines. The equator, the poles, and the central meridian are all projected as straight lines. The length of the central meridian is 0.5072 times the length of the projected equator, and the length of the polar line is 0.5322 times the length of the equator. The graticule is symmetrical along the equator and the central meridian. It is neither conformal nor equal-area, which will cause shape, area, distance, direction, and angle distortion. Area distortion increases with increasing latitude, but is not affected by changes in longitude. High latitudes will be exaggerated. Angular distortion is moderate near the center of the map and increases toward the edges. Distortion values are symmetrical along the equator and the central meridian.
2025-09-16 14:47:01Wagner Projection
The Wagner Projection is a modified azimuthal projection developed by Winkel in 1921. It is essentially a projection of a sphere on a plane, designed to minimize three types of distortion: area, direction, and distance. The projection is neither equal-area nor conformal, and its main feature is that all latitudes are curved except for the poles and the equator, which are straight lines. Its design is achieved through graphic design rather than mathematical equations, and it has certain characteristics in terms of visual balance and global deformation, but it has disadvantages such as non-equal areas and non-conformal angles. In local areas or specific applications, characteristics such as area, shape, and angle may be significantly distorted.
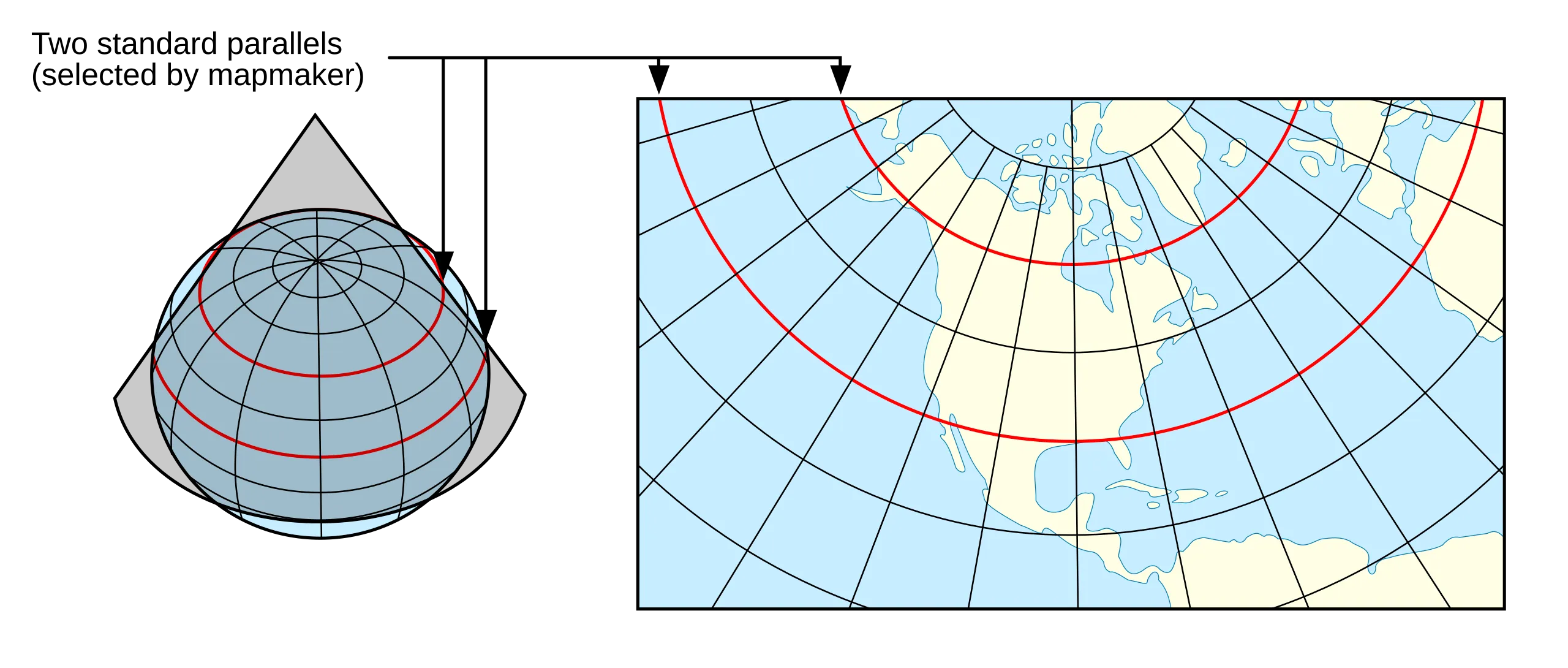
2025-09-16 14:47:01Lambert Conformal Conic Projection
Lambert Conformal Conic Projection is a conic projection method that projects the earth’s surface onto a cone and then unfolds the cone into a flat map. This projection method was developed by French mathematician Johann Heinrich Lambert and is widely used because it is particularly suitable for map making in mid-latitude areas.
2025-09-16 14:47:02Miller Cylindrical Projection
Miller Cylindrical Projection is a map projection method that projects the earth’s surface onto a two-dimensional plane. Its characteristic is that it emphasizes the left-right symmetry (mirror effect) of geographic information. This method is mainly used in scenes that value visual balance and overall grasp. It does not focus on the distance or shape from a specific center point, but focuses more on overall visibility and comparability.
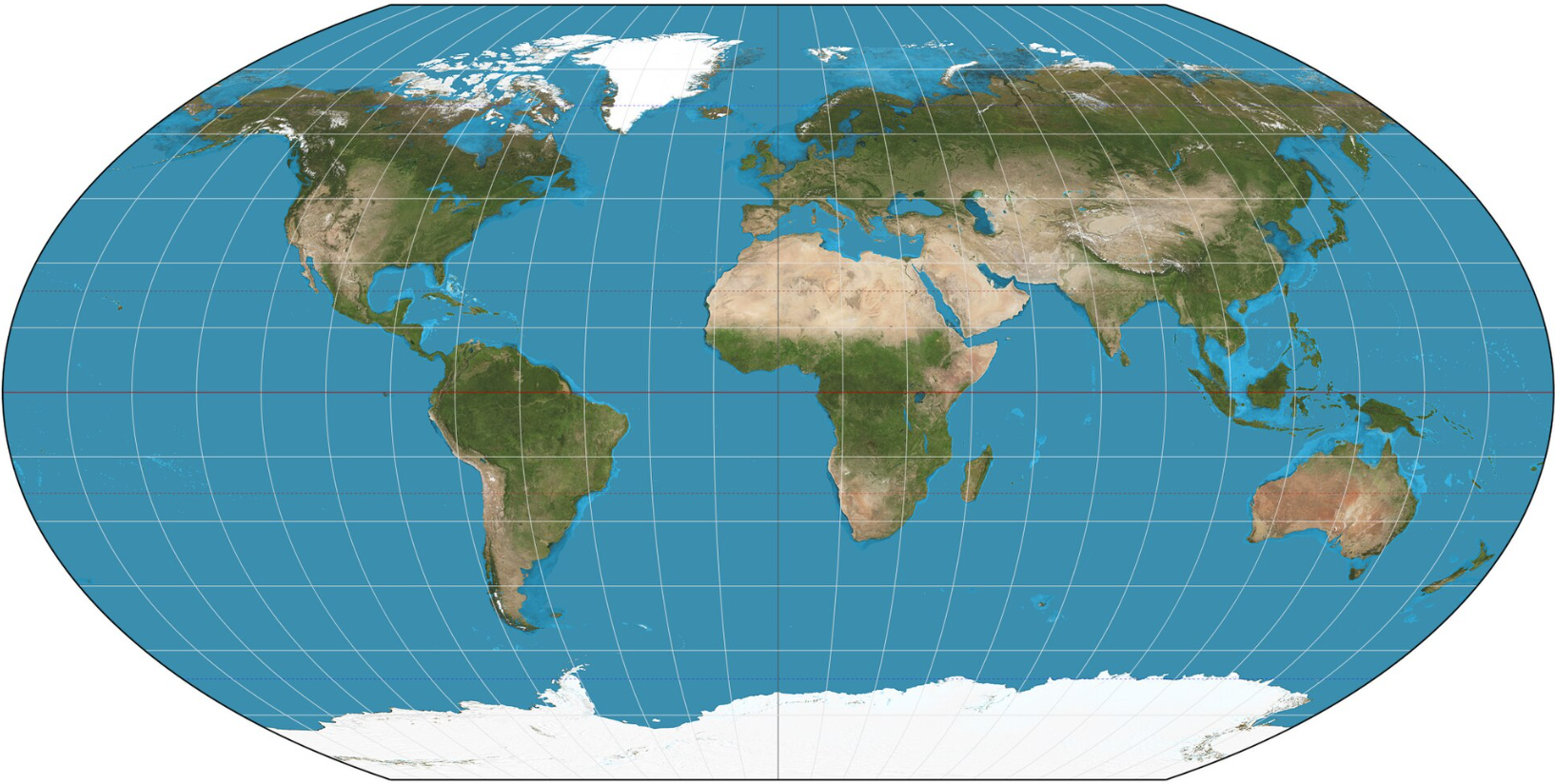
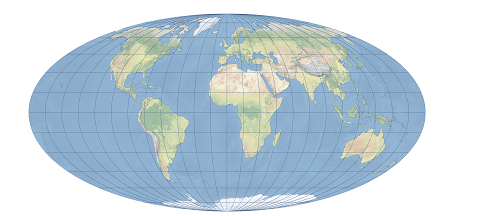
2025-09-16 14:47:02Mollweide Projection
Mollweide Projection is an equal-area pseudocylindrical projection proposed by German mathematician Karl Brandan Mollweide in 1805. The projection maps the earth’s surface onto a flat surface through mathematical transformation, aiming to maintain the accuracy of area ratio while minimizing the distortion of shape and direction. The central meridian of the Mollweide projection is a straight line, the other meridians are symmetrical elliptical arcs, the parallels are parallel straight lines, and the length of the equator is twice the length of the central meridian.
2025-09-16 14:47:03Sinusoidal Projection
Sinusoidal projection is a pseudo-cylindrical equal-area projection created by French cartographer Samson in 1650. It is also called the Samson projection or the Samson-Flamsteed projection. Its core features are that the latitudes are equidistant parallel straight lines, the meridians are sinusoidal curves symmetrical to the central meridian, the central meridian is a straight line with a length ratio of 1, and the equator is a non-deformed line, which can effectively maintain the accurate area ratio. After projection, the length of the equator is twice that of the central meridian, the poles are projected as points and form protruding edges, and the graticule is symmetrically distributed along the equator and the central meridian.
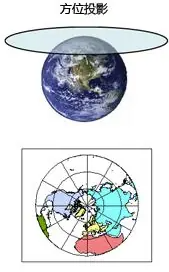
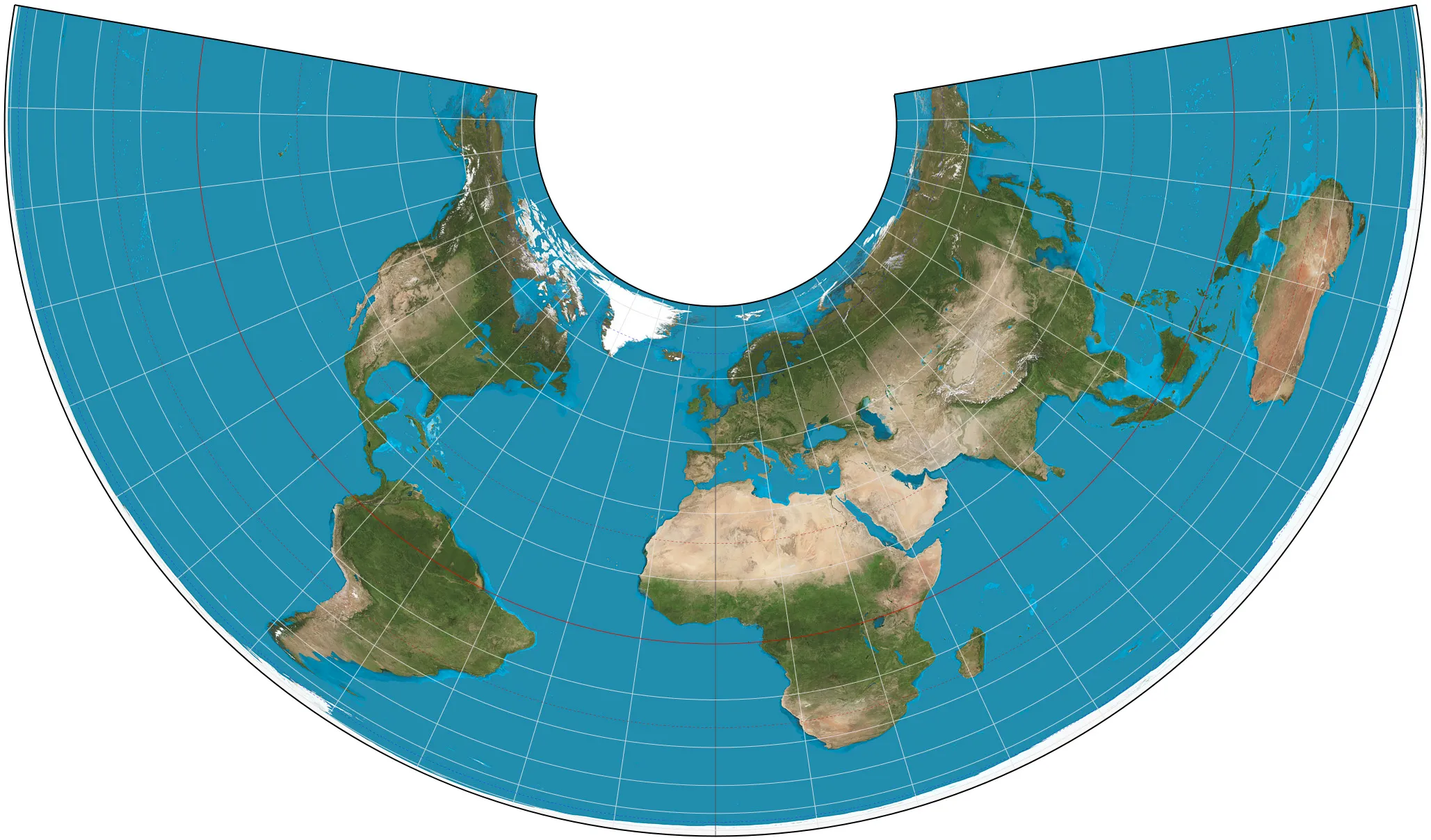
2025-09-16 14:47:03Polar Stereographic Projection
The polar stereographic projection is a method of projecting the earth’s surface onto a plane. With the pole as the center, the points on the earth’s surface are projected onto a plane tangent to the pole through rays. The core principle is to regard the earth as a sphere, with the pole as the viewpoint, the projection surface as a plane tangent to the pole, the meridians projected as radial straight lines, the latitudes projected as concentric circles, and the meridians and latitudes intersecting at right angles, presenting a spider web shape. This projection method can keep the local angles and shapes unchanged, with less deformation in polar regions, and can accurately maintain the relative distance relationship between points on the earth’s surface, ensuring that the direction on the map is consistent with the actual geographical direction.
2025-09-16 14:47:03
 Service
Service