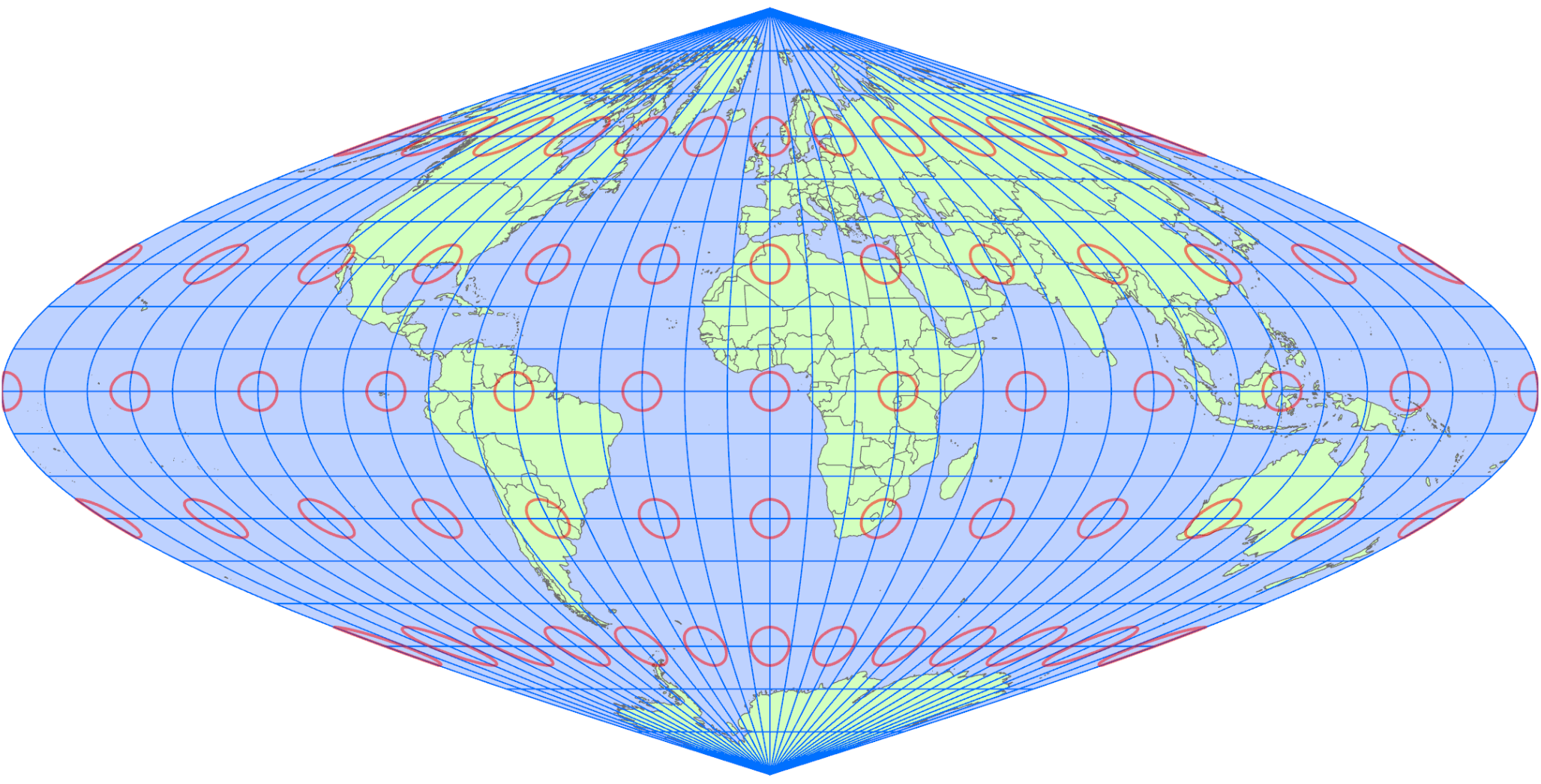
Foucault Sinusoidal Projection
Dec 29,2025

GISBox is a one-stop 3D GIS data editing, conversion and publishing platform that supports editing in multiple GIS formats such as OSGB/GEOTIFF/RVT, converting to 3DTiles/Terrain and publishing.

Introduction

Foucalut Sinusoidal Projection is a type of pseudocylindrical projection proposed in the 19th century by the French physicist Léon Foucault. It is based on the sinusoidal projection and is characterized by the introduction of a correction coefficient to adjust distortion in the latitudinal direction. This projection aims to improve shape balance from low to mid-latitudes while maintaining overall equal-area properties, making it suitable for thematic and statistical maps that display the entire world.

Projection Basic

Foucault Sinusoidal Projection is a mathematically defined projection composed of the following elements:

Central Meridian: The reference meridian for the projection, typically set at 0 degrees longitude. Distortions in distance and shape are minimized along this meridian.
Parallels (Latitude Lines): Parallels are represented as horizontal straight lines spaced evenly, making latitudinal distance relationships intuitive to grasp.
Meridians (Longitude Lines): Meridians are drawn in a sinusoidal curve, spaced widely near the equator and converging toward higher latitudes. In the Foucaut projection, the curvature of the meridians is adjusted by adding correction terms to the sinusoidal projection.
Correction Coefficient (Adjustment Parameter): Introduced as a blend of the characteristics of the sinusoidal projection and the equidistant cylindrical projection, it helps improve shape distortion and visual balance.
Equal-Area Property: The ratio of surface areas on the Earth is preserved on the map, making it suitable for comparing statistical quantities or distributions.

Pros

Preservation of Equal-Area Properties: Areas are accurately represented, making it suitable for quantitative comparisons such as population distribution or land use.
Better Shape Balance Than Sinusoidal Projection: The correction coefficient reduces horizontal distortion in mid-latitude regions, enabling the creation of visually stable world maps.
Relatively Simple Structure: The mathematical definition is clear, making it easy to implement in GIS software.
Suitable for Displaying the Entire World: Lacks extreme area exaggeration and is well-suited for global-scale thematic maps.

Cons

Not Conformal: Since it is not an equal-angle projection, local shapes and angles are not accurately represented.
Distortion in High-Latitude Regions: Strong convergence of meridians near the poles makes landmasses appear stretched horizontally.
Lacks Distance Consistency: Distances in specific directions are not accurate, making it unsuitable for navigation purposes.
Not Widely Used in Practice: Compared to projections like the Mercator or Mollweide, its adoption as a standard map projection is limited.

Application Scenario

The Foucaut Sinusoidal Projection is used in global thematic or statistical maps where both accurate area representation and visual balance are prioritized. It is particularly suitable for illustrating global spatial distributions such as population, climate zones, vegetation, or environmental indicators. It effectively represents mid-latitude regions, where distortion in the sinusoidal projection might be noticeable, in a more natural form. This projection is valuable in academic materials, educational contexts, and conceptual visualizations of analytical results where both quantitative accuracy and an overall global perspective are required.