August Epicycloidal Projection
Dec 29,2025
GISBox is a one-stop 3D GIS data editing, conversion and publishing platform that supports editing in multiple GIS formats such as OSGB/GEOTIFF/RVT, converting to 3DTiles/Terrain and publishing.
Introduction
August Epicycloidal Projection is a pseudazimuthal world map projection devised by mathematician Ferdinand August in the 19th century. This projection is characterized by the arrangement of meridians and parallels based on epicycloid curves, with the aim of representing the entire world on a single map. While it does not strictly preserve area, angles, or distances, it offers overall visual balance and a unique geometric beauty, making it primarily suitable for theoretical and educational purposes or the study of map projections.
Projection Basic
August Epicycloidal Projection is not a data format with a specific file structure but a map projection based on mathematical definitions, composed of the following geometric and mathematical elements:
- Reference Shape (Epicycloid): The outer boundary of the projection is defined by an epicycloid curve, and the entire world map is drawn within this curve.
- Central Point (Projection Center): The intersection of the equator and the prime meridian is typically placed at the map’s center, from which distortions radiate outward.
- Meridian Arrangement: Meridians are drawn as curves, remaining relatively even near the center but curving significantly toward the edges.
- Parallel Arrangement: Parallels are also represented as curves rather than straight lines, arranged along the shape of the epicycloid.
- Mathematical Model: The projection is defined by parametric equations in analytical geometry and is reproduced in GIS software or map-drawing libraries through formula implementation.
Pros
- Unique and Impressive World Representation: The appearance based on the epicycloid shape is highly distinctive and easily distinguishable from other world map projections.
- Ability to Depict the Entire World on a Single Map: The entire globe, including polar regions, can be represented within a single closed curve, making it suitable for presenting the concept of the world.
- Educational Value for Understanding Projections: The distribution of distortions is intuitively graspable, making it useful for comparing map projections or explaining their mathematical foundations.
- Suitable for Decorative and Illustrative Purposes: Effective in contexts where visual appeal is prioritized, such as scientific illustrations or exhibition maps.
Cons
- Does Not Preserve Area, Angles, or Distance: It satisfies none of the properties of equal-area, conformal, or equidistant projections, making it unsuitable for quantitative analysis.
- Significant Distortion at the Edges: Shape distortion becomes pronounced near the projection boundaries, making geographical comparisons difficult.
- Limited Use in Practical GIS Applications: Lacks a standard EPSG code and often requires customization in most GIS software.
- Low Intuitiveness for Positional Relationships: The strong curvature of meridians and parallels makes it challenging for general users to grasp geographical positions.
Application Scenario
The August Epicycloidal Projection is not used for precise geographical analysis or surveying but is primarily employed in academic and educational contexts to introduce or compare map projection methods. It is often used as teaching material in cartography and geodesy at universities and research institutions, as well as in explanatory diagrams for the history of maps or mathematical visualization. It is also adopted in settings where visual impact is prioritized, such as exhibition panels or book illustrations. Rather than for practical geographic information processing, it is positioned as a symbolic representation of the diversity of projection methods and the possibilities of map expression.
Example
1. Example of the August Epicycloidal Projection.
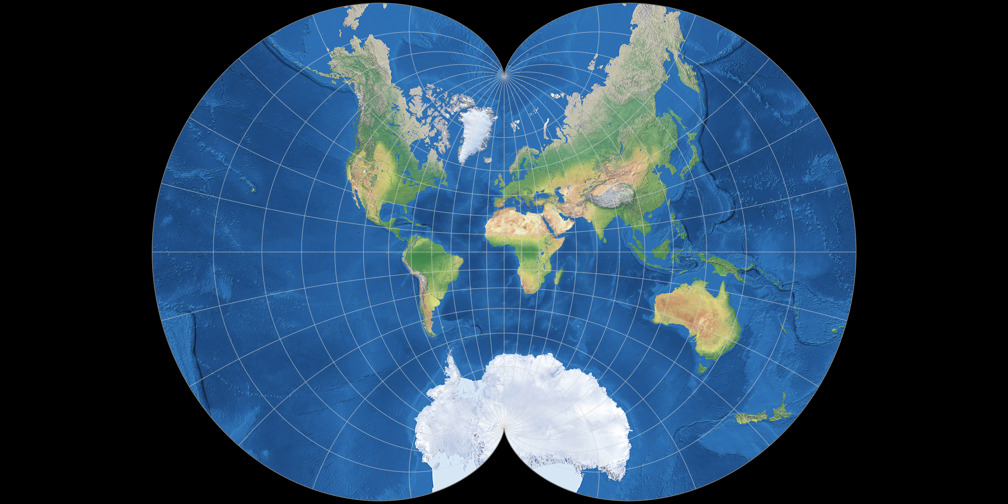
2. Example of the August Epicycloidal Projection.
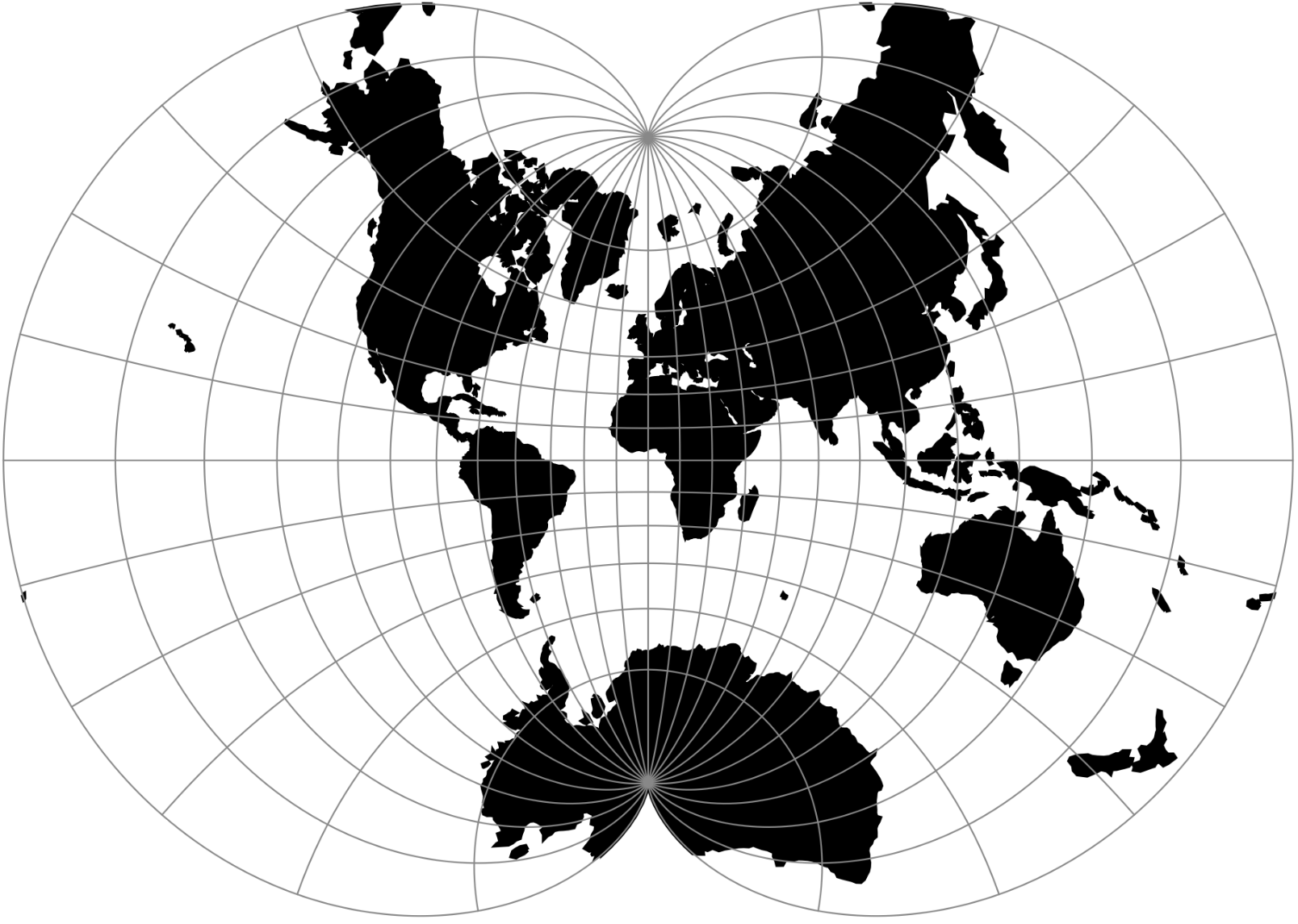
Related GIS Projections
Vertical Near-side Perspective Projection
Two-point Equidistant Projection

 Service
Service
