Armadillo Projection
Dec 29,2025
GISBox is a one-stop 3D GIS data editing, conversion and publishing platform that supports editing in multiple GIS formats such as OSGB/GEOTIFF/RVT, converting to 3DTiles/Terrain and publishing.
Introduction
Armadillo Projection is a relatively new world map projection designed to represent the entire Earth on a single plane in a visually striking manner. It prioritizes visual continuity and artistic expression over geometric accuracy, featuring a unique shape that appears to wrap around the globe. Primarily used for educational purposes, design, and visualization, it is known as a projection that offers a fresh perspective on presenting geographic information.
Projection Basic
The Armadillo Projection is not a file format or data structure but a mathematical map projection, composed of the following theoretical elements:
- Reference Sphere: Treats the Earth as an ideal sphere, using longitude and latitude as the basis for projection calculations.
- Projection Center and Transformation Functions: Employs a set of nonlinear mathematical formulas to transform coordinates from the Earth's surface onto a plane, maintaining a continuous shape during the process.
- Boundary Shape Definition: The resulting projection does not take a rectangular or circular form but features an organic outline reminiscent of an armadillo's shell.
- Distortion Distribution Model: Adopts a design philosophy that disperses distortions in area, distance, and angles across the entire map rather than concentrating them in specific regions.
- Emphasis on Central Regions: The central area of the projection exhibits high visual continuity, making it easier to intuitively grasp the interconnectedness of the world.
Pros
- High Visual Impact: Its shape differs significantly from conventional world maps, capturing viewers' attention and sparking interest in geography.
- Intuitive Representation of Continental Continuity: Oceans and continents are arranged with minimal breaks, allowing for a cohesive understanding of the Earth's interconnectedness.
- Suitable for Education and Visualization: Effectively conveys geographic concepts flexibly in contexts that prioritize comprehension and creativity over precision.
- Compatibility with Art and Design: Excels when treating maps not only as informational media but also as visual expressions.
- Challenges Traditional Projections: Offers a new perspective on established worldviews, such as the Mercator projection.
Cons
- Unsuitable for Surveying and Analytical Purposes: Does not strictly preserve area, distance, or angles, making it inadequate for quantitative analysis.
- Lacks Standard EPSG Code: Not natively supported by mainstream GIS software, requiring custom implementation.
- Non-Intuitive Distortion Properties: Difficult for non-experts to understand the extent of distortion in different regions.
- Unsuitable for Printing or Tiled Display: The non-rectangular shape makes it challenging to divide into pages or tiles.
- Limited Practical Use Cases: Primarily confined to experimental or expressive purposes, with few examples of adoption in administrative or engineering fields.
Application Scenario
The Armadillo Projection is utilized in contexts where visually presenting the Earth as a whole takes precedence over precise measurement, such as geographic education, exhibition panels, and visual representations of world maps in books or websites. It is particularly effective in offering a fresh perspective to viewers accustomed to traditional world maps and challenging geographic stereotypes. Additionally, it is often symbolically used in data visualization and art projects that aim to merge geographic information with design.
Example
1. World Rice Armadillo Projection.
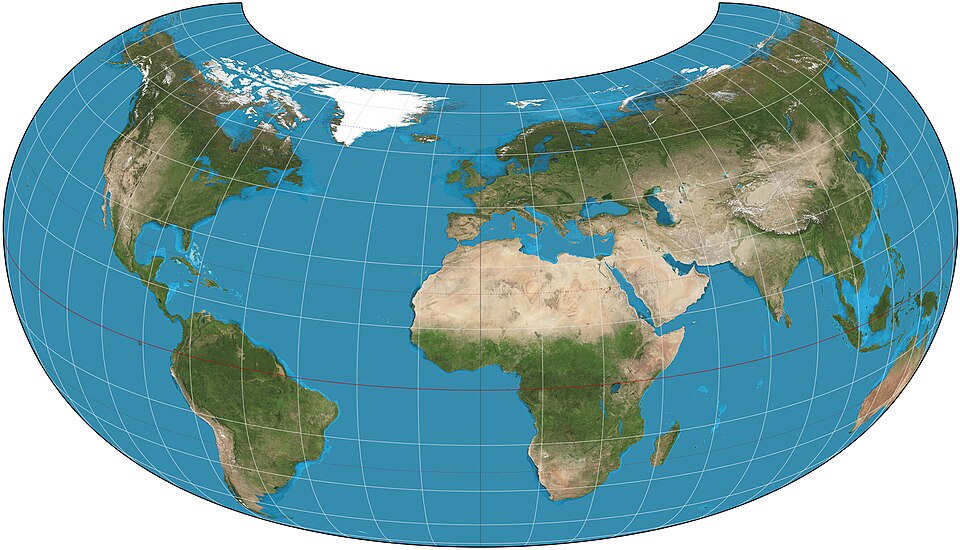
2. The Armadillo Projection, invented by Hungarian engineer Erwin Raisz, is a creative and beautiful solution for depicting a 3D globe on paper.
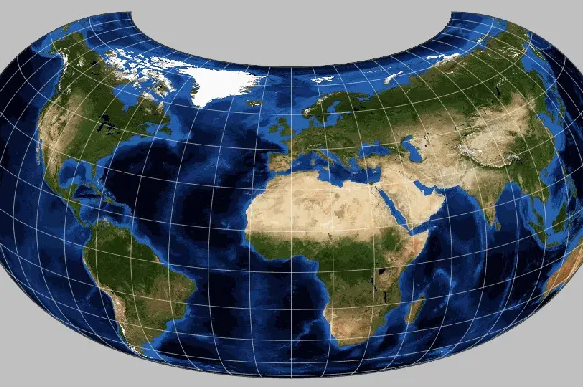
Related GIS Projections
Vertical Near-side Perspective Projection
Two-point Equidistant Projection

 Service
Service
