ワンストップ型の軽量GISプラットフォーム、3つの強力機能を搭載

アルベルス正積円錐図法（Albers Equal-Area Conic Projection）は、面積を正確に保つ円錐図法の一種であり、地理情報システム（GIS）や地図製作において広く使用される投影法の一つです。

心射図法は、地球の中心から地表上の任意の点へ直線を引き、それが地球と接する平面と交わる点に投影される方法です。これは透視投影（中心投影）の一種であり、地球上の「大円航路（最短ルート）」が、投影後には直線として表されるという特徴があります。このため、直線で最短距離を示したい場合に非常に有用です。

ミラー図法とは、地球表面を二次元上に投影する際に、地理情報の左右対称性（ミラー）を強調した地図投影法の一種です。主に視覚的なバランスや全体把握を重視する場面で用いられ、特定の中心点からの距離や形状の保存よりも、全体的な視認性や比較性に重きを置いた設計になっています。

Web Mercator（EPSG:3857 または EPSG:900913）は、主にインターネット地図サービス（例：Google Maps、Bing Maps、OpenStreetMap など）で広く使われている地図投影法です。「Pseudo Mercator（擬似メルカトル）」とも呼ばれ、本来のメルカトル投影（正確な航海用地図投影）とは数学的に少し異なる簡易版のメルカトル投影です。

ステレオ投影とは、地球の表面や球面上の点を、球の一つの点（通常は極点）から平面に投影する手法です。この投影法は、点を球面上に配置し、ある一点から対極に位置する投影面に投影することで、円形の地図として表現します。古代ギリシャの数学者によって考案され、天文学や結晶学、地図作成など幅広い分野で使用されています。

ロビンソン図法は、1963 年にランドマクナリー社の依頼によりアーサー・H・ロビンソンによって設計された妥協型の地図投影法です。この図法は数学的な方程式ではなく、グラフィックデザインによって開発され、世界地図において視覚的にバランスの取れた表現を実現することを目的としています。

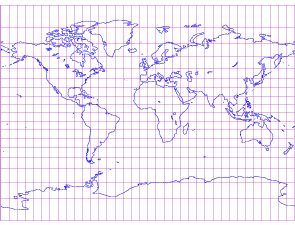
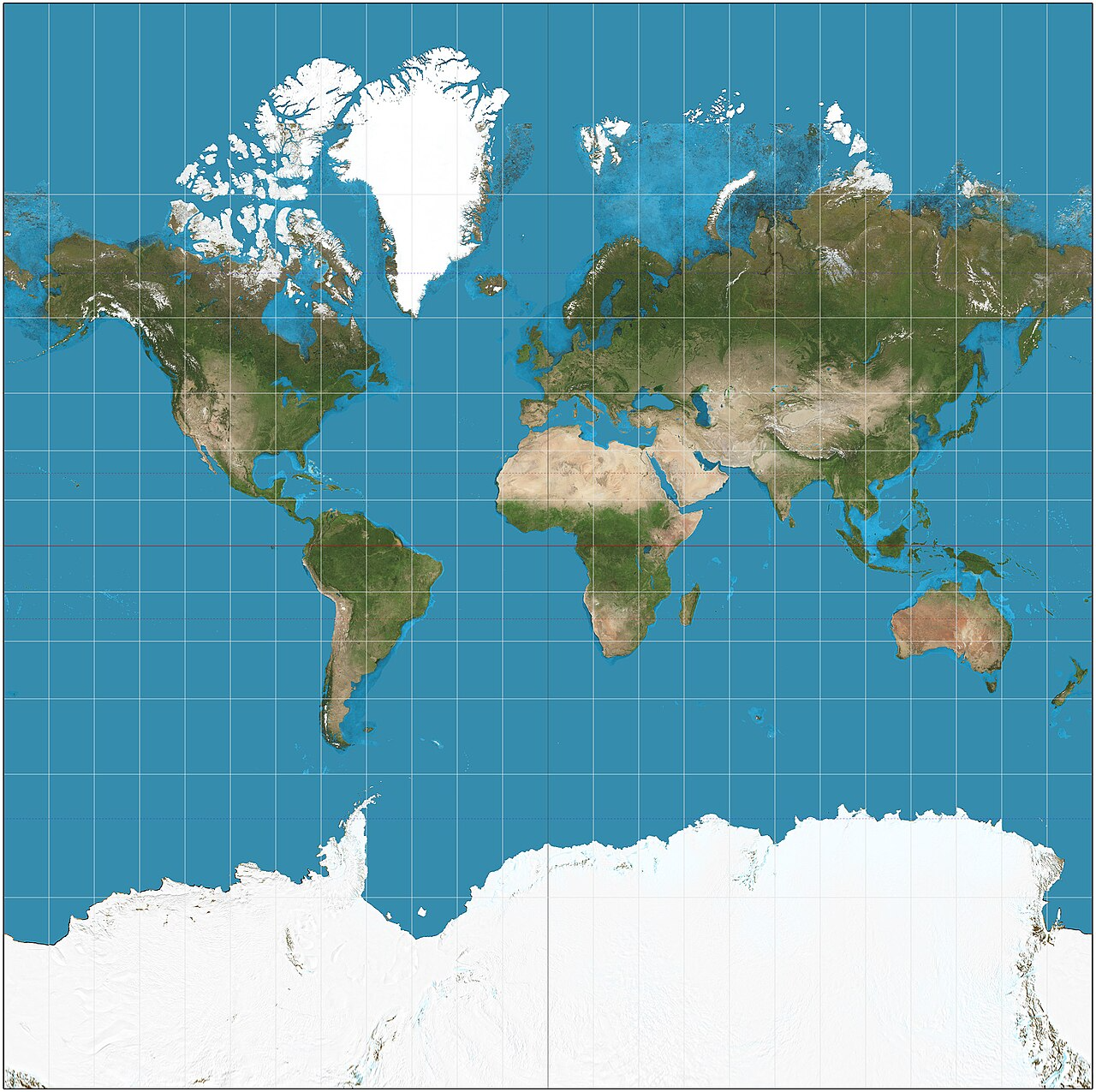
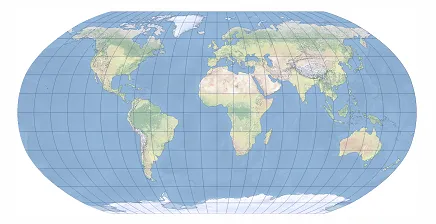
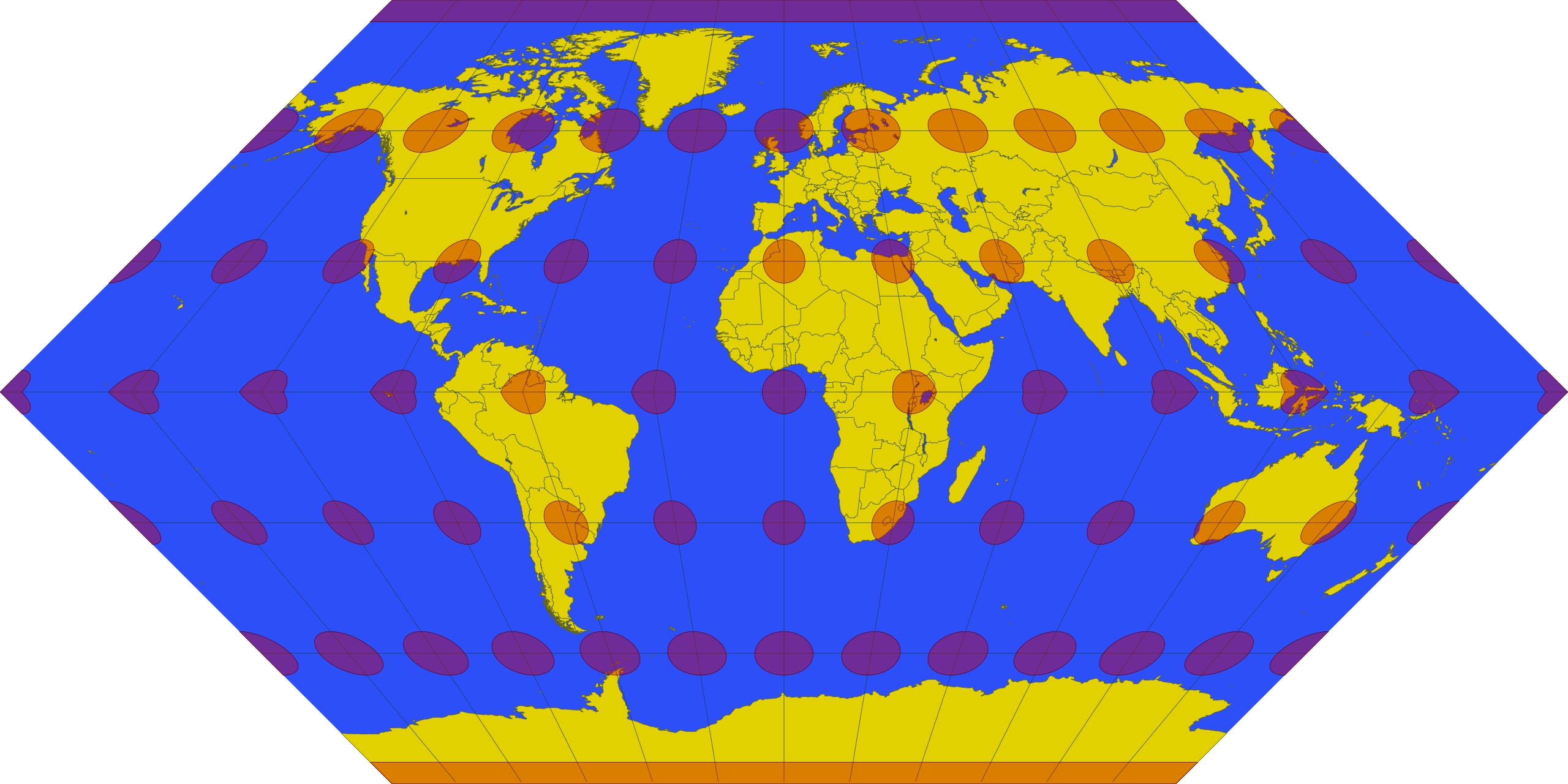
メルカトル図法（Mercator Projection）は最も有名な地図投影法の一つで、もともとフランツ・ヴァルター・メルカトル（Gerardus Mercator）によって 1569 年に提案されました。主に航海図の作成に利用されるこの投影法は、正軸等角円筒投影とも呼ばれ、「標準等角円筒投影」とも称されます。特徴として、地球の経緯度座標を平面上に投影し、角度を維持することができるため、航海および航空ナビゲーションに非常に有用です。メルカトル図法では、地球の表面を円筒として扱い、経緯線をこの円筒に写し取った後、「展開」して平面図を作成します。この投影法では角度を維持するため、「等角投影」とも呼ばれます。

エッケルト図法は、20 世紀初頭のドイツの地理学者マックス・エッケルト（Max Eckert）によって考案された地図図法の総称です。彼は異なる特性を持つ 6 種類の図法（Eckert I ～ Eckert VI）を開発しており、それぞれが地球の表面を異なる視点から表現しています。これらの図法は主に擬円筒図法に分類され、特にエッケルト IV と VI は、面積の正確さ（正積性）と視覚的なバランスの良さから、教育や地理資料に広く使用されています。

正距円錐図法は、地球を円錐面に投影し、地図として表現する円錐投影法の一種で、経線（子午線）と緯線の間隔を一定に保つことが特徴です。特に、標準緯線と呼ばれる一つまたは二つの緯線上では、距離の歪みが最小となるよう設計されています。

ファン・デル・グリンデン図法（Van der Grinten Projection）は、1898 年にアメリカの地理学者アルフォンス・ファン・デル・グリンデン（Alphons J. van der Grinten）によって開発された世界地図投影法です。この図法は、地球全体を一つの円の中に収めることができるという特徴を持ち、経線と緯線を曲線として描写することで、視覚的にバランスの取れた世界地図を提供します。メルカトル図法と比べて極地の歪みを抑えつつ、大陸の形状を比較的自然な印象で表現できることから、アメリカ地質調査所（USGS）などの地図にも採用された歴史があります。